The Sun is the biggest celestial object in the Solar System. We see it as a big bright dot of light in the sky; however, the Sun is enormous, capable of hosting all the planets within it, and much more!
So, how big is the Sun? More than one million Earths could fit inside the Sun if it were hollow. The Sun has a radius of 696.340 km / 432.685 mi and a diameter of 1.39 million km / 864.000 mi.

Earth, for comparison, has a radius of only 2.439 km / 1.516 mi, and a diameter of just 12.742 km / 7.917 mi. All the planets in our Solar System combined account for just 0.2% of the Sun’s mass. Earth, for example, is 330.000 times less massive than the Sun.
Other Comparisons
To put that into perspective, the mass of Earth is equivalent to 5.9 quadrillion kg. But how do the other stars fare? The most giant planet in our Solar System, namely Jupiter, has a diameter of around 142.984 km / 88.846 mi at the equator, and a diameter of about 133.708 km / 83.082 mi at the poles. It has a mean radius of 69.911 km / 43.440 mi, and its mass is equivalent to 318 Earth masses. You could fit 1.300 Earths inside Jupiter.

Now that may seem impressive at first glance; however, consider this. You could fit 1,000 Jupiter’s inside the Sun. Now let’s take a look at Mercury, the smallest planet in our Solar System.
Mercury has a diameter of only 4.879 km / 3.032 mi and a radius of 2.439 km / 1.516 mi and only 0.055 Earth masses. It would take around more than 21.2 million Mercury-sized planets to fit inside the Sun. With that being said, what is bigger than our Sun?
What Is Bigger than the Sun?
The Sun may seem incredibly big, but there are billions of things in the Universe, which are bigger than our Sun. Consider this; our Sun is considered an averaged sized star in the best-case scenario.
There are enormous stars out there which are hundreds to thousands of times bigger than our Sun. These stars are known as giant stars, supergiant stars, or hypergiant stars.
Let’s take a look at one of the most famous giant stars, VY Canis Majoris. VY Canis Majoris has between 1,300 to 1,540 solar radii, which means its radius, is at least 1,300 times that of our Sun’s.
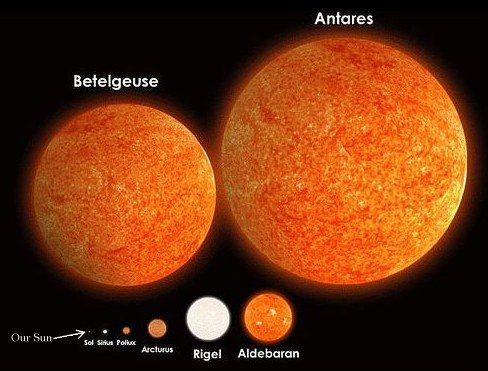
Another star, KY Cygni, has between 1,420 and 2,850 times the radius of our Sun. UY Scuti has 755 solar radii, WHO G64 has between 1,504 and 1,730 times the radius of the Sun.
Mu Cephei has around 1,650 times the radius of the Sun, while RW Cephei has 1,535 times the radius of the Sun. Westerlund 1-26 has between 1,530 and 2,550 times the radius of the Sun, while V 354 Cephei has 1,520 times the radius of the Sun.
As you can see, there are plenty of stars which are several times bigger than our Sun out there. It’s just a matter of time until we will reclassify our Sun as being below average- in terms of size.
How Big is Betelgeuse Compared to the Sun?
Betelgeuse, like the other stars mentioned above, is among the biggest stars in our Universe that we know of at least. This supergiant red star has between 950 and 1,200 solar radii, or it has between 95.000% and 120.000% of our Sun’s radius. You could easily fit more than 8 billion Sun’s inside Betelgeuse.

What is the Sun Made of?
The Sun is basically a big ball of gas, being made by around 91% hydrogen and 8.9% helium, in regards to atoms. When it comes to the Sun’s mass, it is made out of 70.6% hydrogen and 27.4% helium.
The Sun’s mass is enormous, being 330.000 times than our Earth’s mass, which is 5.9 quadrillion kg. This mass is held together by gravity, and it produces great pressure and temperatures at its core.
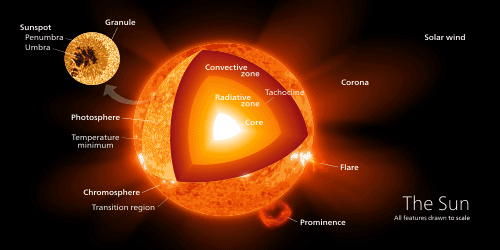
Six regions comprise our Sun, namely the core, the radiative zone, the convective zone; these are the interior regions, followed by the photosphere, chromosphere, and the outer region, which is called the corona.
Inside the Sun, temperatures are unphatomable, especially at its core. The Sun’s core temperature is estimated to be around 27 million degrees Fahrenheit / 15 million degrees Celsius.
Is the Sun Getting Bigger?
The Sun is getting both bigger and hotter, and this is because it continues to burn hydrogen into helium at its core. The core is in the process of collapse, as it heats up, and this causes the Sun’s outer layers to expand.
This process is quite natural and nothing to worry about. All the stars go through this process since they are born, and through our Sun’s lifetime, it has expanded by about 20% since its formation, in the best case.
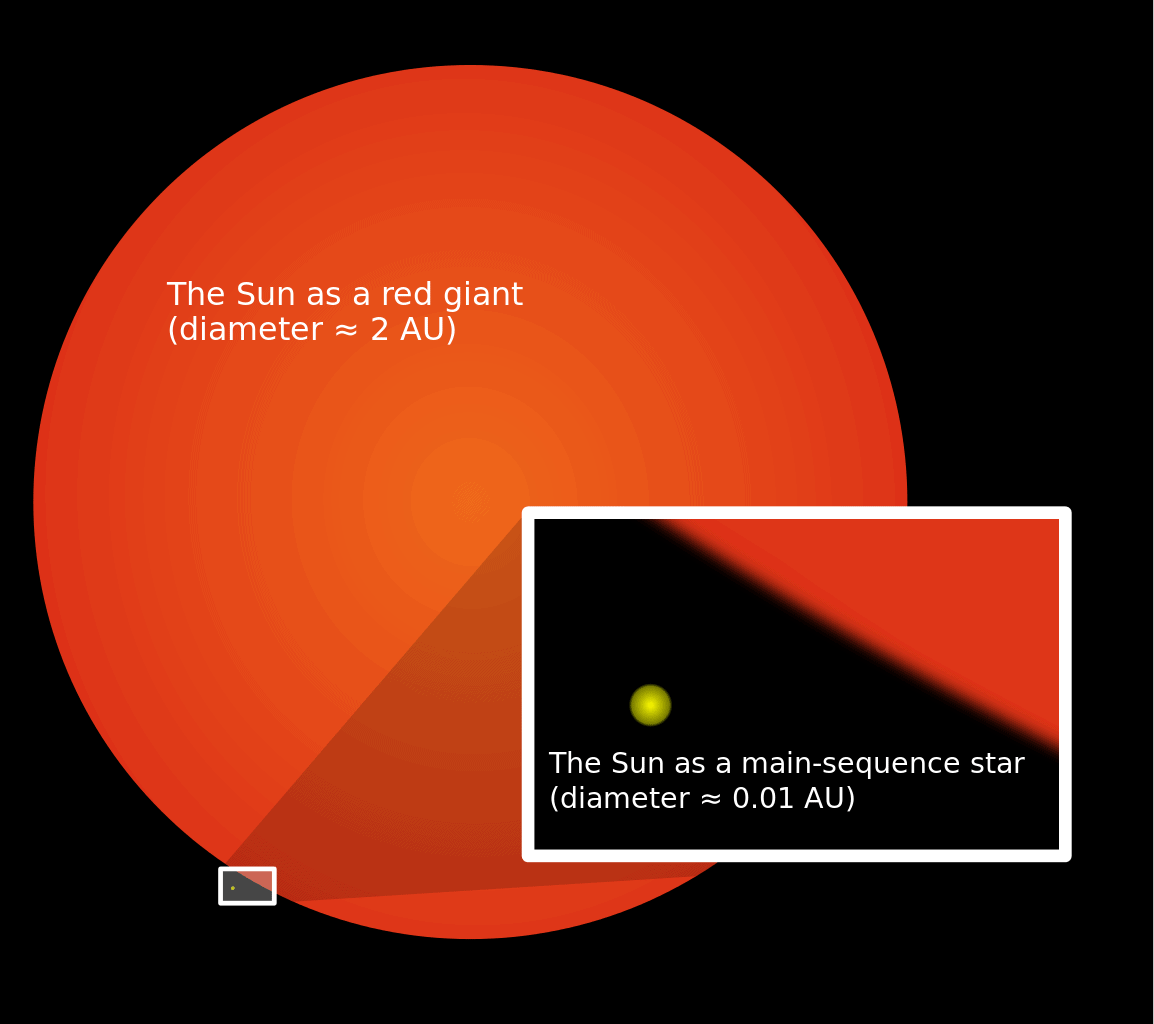
In the distant future, our Sun will become what is known as a red giant star. This will happen in about 5 billion years as the Sun will start its helium-burning process. When this happens, our Sun will expand several times its current size and engulf the planets Mercury, Venus, and even Earth.
What Color is the Sun?
We are accustomed to believing that our Sun is yellowish in color, but it isn’t. So what is the color of the Sun then? Believe it or not, our Sun is actually white, and the majority of images you see that portray our Sun are altered to appear as yellow, or even orange.
These images are altered by scientists to make it easier for us to recognize our Sun. But why does the Sun appear yellow? It all has to do with Earth’s atmosphere.

Our Sun emits every color, but if you were to see it from outer space, it would be a big white ball of light. The atmosphere of Earth acts like a filter, leaving out the cool light spectrum and amplifying the warmer colors. The filtered blue light refracts from atmospheric molecules, contributing to our sky’s appearance of blue.
What is the Biggest Star Known Today?
For a long period of time, the biggest star known to us was either VY Canis Majoris, Betelgeuse, or UY Scuti; however, since 2020, the biggest star we currently know of is Stephenson 2-18.
Stephenson 2-18 is genuinely a behemoth, having 2,150 times the radius of the Sun (This is currently the largest star discovered in the Universe since 2020).

It would take more than 10 billion Sun’s to fill Stephenson 2-18. But are there any other stars even bigger than Stephenson 2-18? There might as well be! Consider this, Stephenson 2-18 is not even done growing up since it is a relatively young star; it will become even bigger in the near future. As for other giant stars, we might as well discover new ones soon to break the record.
Did you know?
- The Sun has already lived almost half of its life, it is 4.5 billion years old, and in about 5 billion years, it will become a red giant.
- When our Sun will end its red giant phase, it will begin to shrink, eventually reaching the size of our Earth. It will then become what is known as a white dwarf star.
- If our Sun would suddenly disappear, it would take around 8 minutes for us to realize that. This is because our Sun is very far away, and its light reaches us in 8 minutes, or eight light minutes.
- The Earth is rotating from east to west; however, our Sun is rotating from west to east, in the opposite direction of Earth, and that’s not all. The Sun is actually rotating faster at its equator than at its poles. This is known as differential rotation.
Sources:
Image Sources:
- https://ilovetheuniverse.com/wp-content/uploads/2016/06/Planets_and_sun_size_comparison-1024×575.jpg
- https://theplanets.org/wp-content/uploads/2014/09/sun-size.jpg
- https://i.pinimg.com/originals/c7/2a/32/c72a32a8677d9745041a3f063960b3e4.jpg
- https://sbchouston.files.wordpress.com/2015/12/betelguesesun.png
- https://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/Sun_poster.svg/500px-Sun_poster.svg.png
- https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Sun_red_giant.svg/1154px-Sun_red_giant.svg.png
- https://i.ytimg.com/vi/6fl1JXesYhc/hqdefault.jpg
- https://upload.wikimedia.org/wikipedia/commons/thumb/1/11/Size_Comparison_of_Stephenson_2-18_and_VY_Canis_Majoris.jpg/1280px-Size_Comparison_of_Stephenson_2-18_and_VY_Canis_Majoris.jpg
